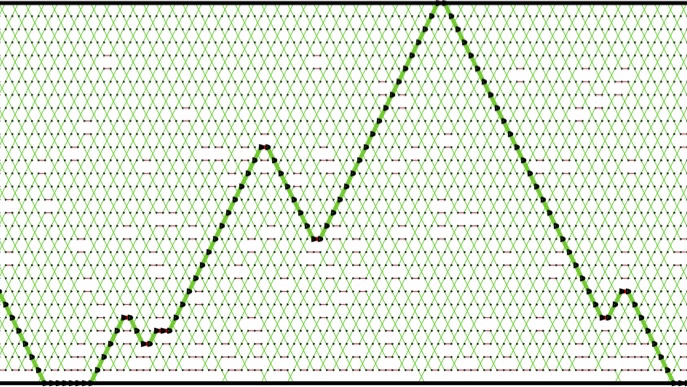
Scalable approximation of complex probability distributions

The prevalence of uncertainty in our world has fuelled the development of sophisticated mathematical methods to understand and tame uncertainty­­­. This has been a central quest in the field of statistics. A key concept often used to depict uncertainty is the notion of a probability distribution, which can be thought of as measuring, for each possible state of the system, a degree of belief. Being able to interrogate probability distributions is therefore of paramount importance in statistics, and hence in the many fields of science and engineering that depend on statistics and uncertainty quantification. As scientific models become increasingly complex, the calculations required to query probability distributions are getting computationally prohibitive, to the point that these computations are the bottleneck in many disciplines. My field of research is concerned with computational methods that break these bottlenecks, by making use of algorithms exploiting randomness.

  JRSSB paper on a new perspective to Parallel Tempering (PT)

  ICML paper on PT with generalized paths of distributions

  NeurIPS paper on PT with adaptive references

  Pigeons: Software for scalable, distributed sampling

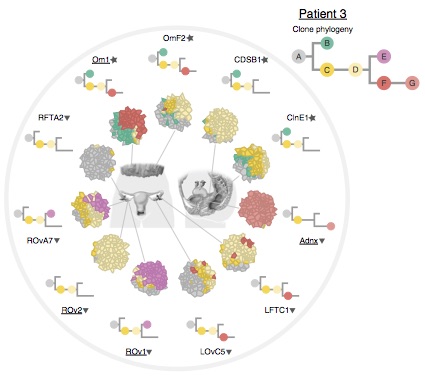
Probabilistic modelling of the evolutionary dynamics and phylogeny of cancer

Proliferating cancer cells, in which DNA repair mechanisms are disrupted, accumulate mutations at a much faster rate than healthy cells do. This leads to the emergence of an evolutionary process inside the tumour. A current research frontier is the characterization of the evolutionary dynamics and phylogenies within individual cancer tumours, where multiple sub-populations of cancer cells acquire differentiating sets of mutations.

  Our Nature paper based on Bayesian Wright-Fisher SDE analysis of fitness of subclonal relative fitness

  Phylogenetic inference from single cell copy number alterations

  Nature Methods paper on the analysis of single cell data

  Nature Methods paper on PyClone, a Bayesian non-parametric deconvolution method for bulk cancer data

  More papers

Tools for Bayesian data science

We are developing a language and software development kit for doing Bayesian analysis. The design philosophy is centered around the day-to-day requirements of real world (Bayesian) data science. The inference engines brings to bear several recent advances such as non-reversible methods.

  Easy to use distributed Bayesian inference

  A modelling language for Bayesian inference over combinatorial spaces

  Software for scalable, distributed sampling

  Blang project site

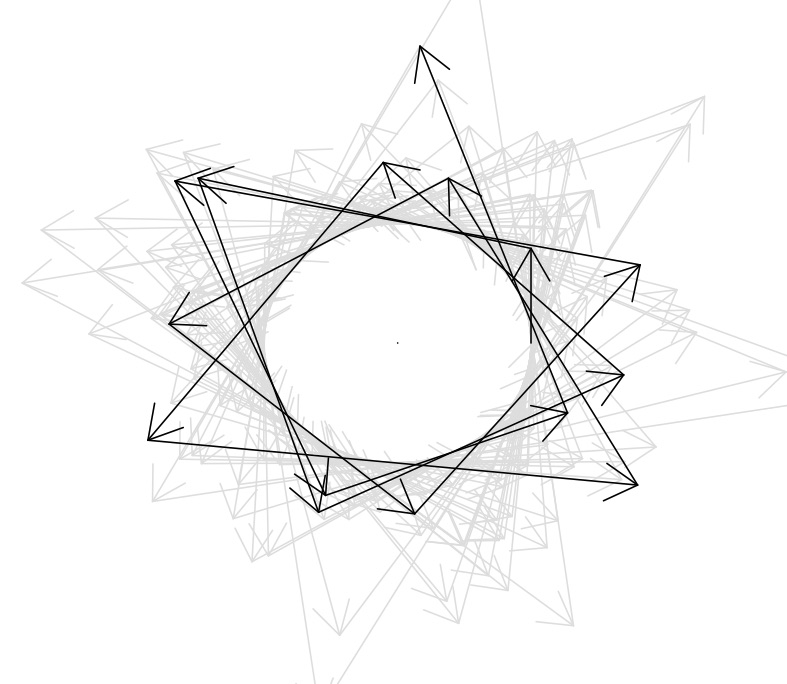
Non-reversible gradient-based Monte Carlo methods

Markov chain Monte Carlo (MCMC) is notoriously difficult to scale to problems having high-dimensional latent variables ("big models"), which arise in many scientific and engineering applications.

  We are working on an alternative to MCMC that we call the "Bouncy Particle Sampler" (BPS), which imports ideas from the field of molecular simulation to scale MCMC to high dimensional problems. JASA paper

  Follow-up Annals of Statistics paper, on the geometric ergodicity of BPS

  Preprint of follow-up work, on non-linear trajectories and discrete piecewise deterministic Markov processes

  Application of BPS to CTMC parameter estimation (in JMLR)

  More information

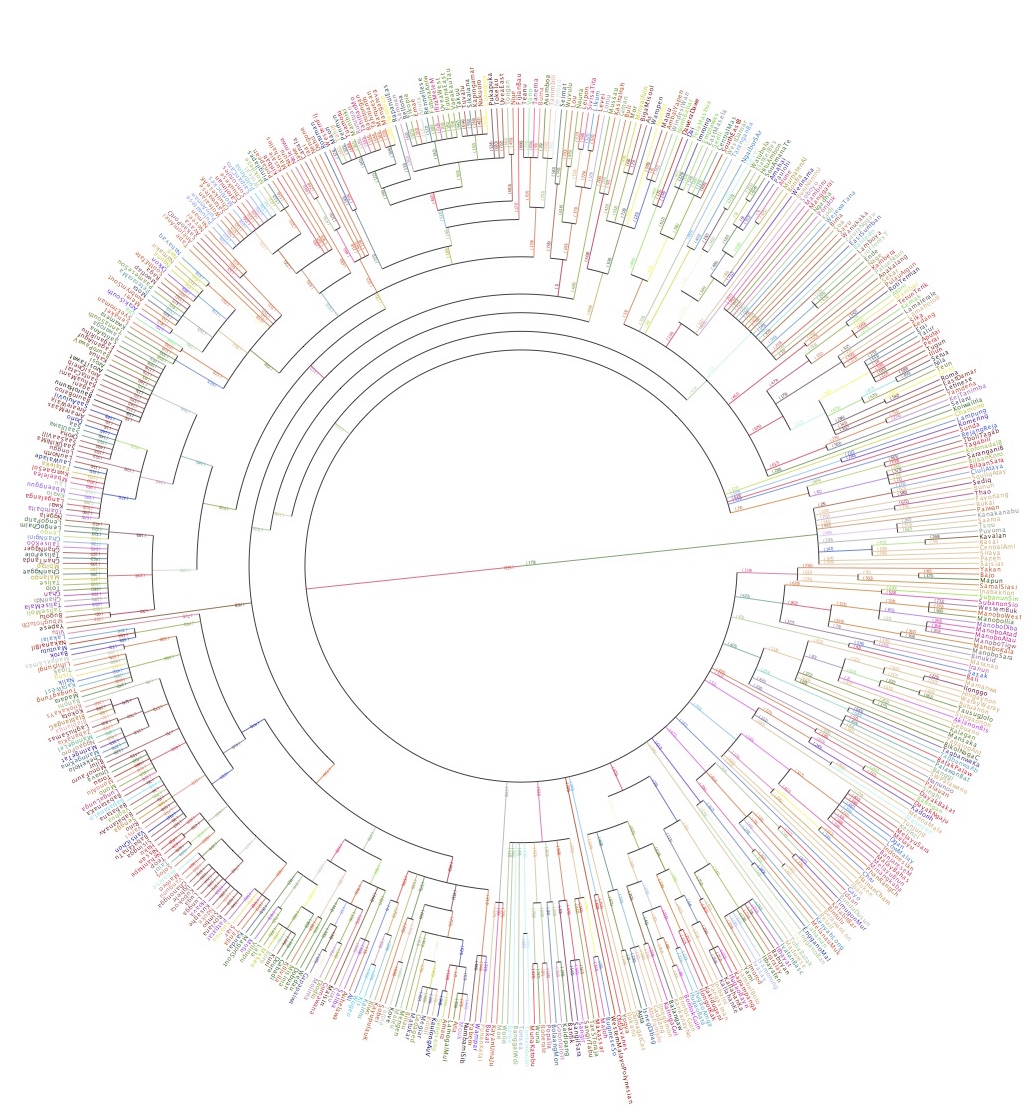
Bayesian phylogenetic inference

As a result of advances in sequencing technologies, the fields of computational and statistical phylogenetics, which are concerned with the modelling and inference of evolutionary relationships, have been growing rapidly in recent years. I am particularly interested in computationally-intensive Bayesian methods and inference of complex evolutionary models.

  Sys Bio paper on change-of-measure based phylogenetic SMC algorithm.

  Novel sampling method based on Hamiltonian Monte Carlo for parameter-rich evolutionary models.

  Long indel model (in Sys Bio) based on the Poisson Indel Process (PNAS).

  More papers

Computational historical linguistics

Phylogenetic trees (or networks, forests, etc) also play an important in linguistics, to describe how language change and splits in ancestral speaker populations gave rise to today's linguistic diversity. Computational methods are also starting to play an important role in this field.

  PNAS paper on automated ancient language reconstruction

  More papers